【印刷可能】 球体 体積 計算 207126-球体 体積 計算

2

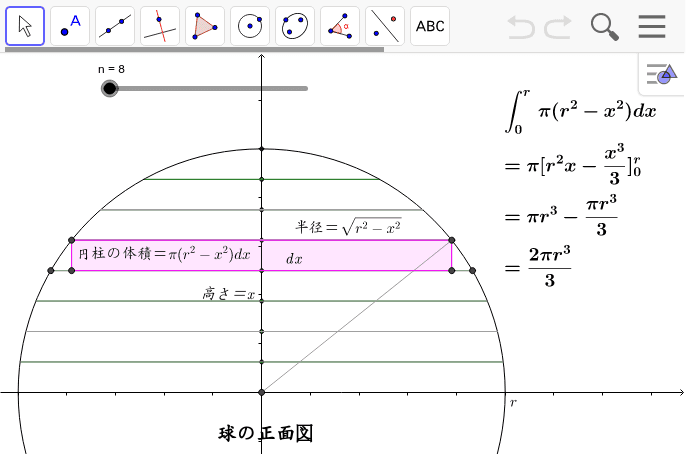
体積 = 半径 × 半径 × 314 × 高さ 公式の 導出 どうしゅつ 方法と計算例は、「 円柱の体積の求め方 」をご覧ください。 円柱の体積の求め方 錐体の体積 錐 すい の体積は、底面積 S S 、高さ h h として、次の式で求められます。 この公式は、底面の形によりません。 錐体 すいたい の体積 V = 1 3Sh V = 1 3 S h 体積 = 底面積 × 高さ ÷ 3 角錐 かくすい と 円錐 えんすい の図を、それぞれ見てみましょう。球の体積の計算 球の体積を計算してみます。 ある点 (中心)から、表面のどの点までの距離も等しい物体を球と呼びます。 球の体積は、中心から表面までの距離 (常に一定)を半径rとすると、 4/3 * π * r3 であらわされます。 πは、円周率のことです。 円周率は と続きます。 実際の計算では、314などのように近似値で行うことがあります。 半径 の球の体積は です。 球の体積を厳密に求

球体 体積 計算

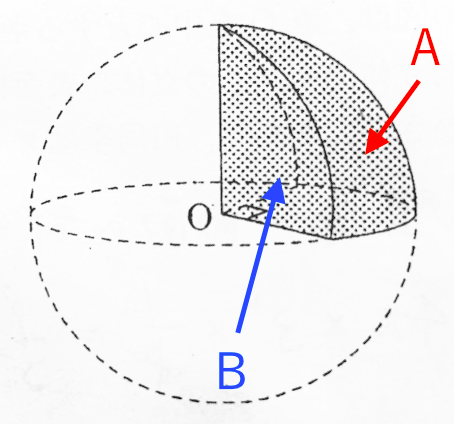
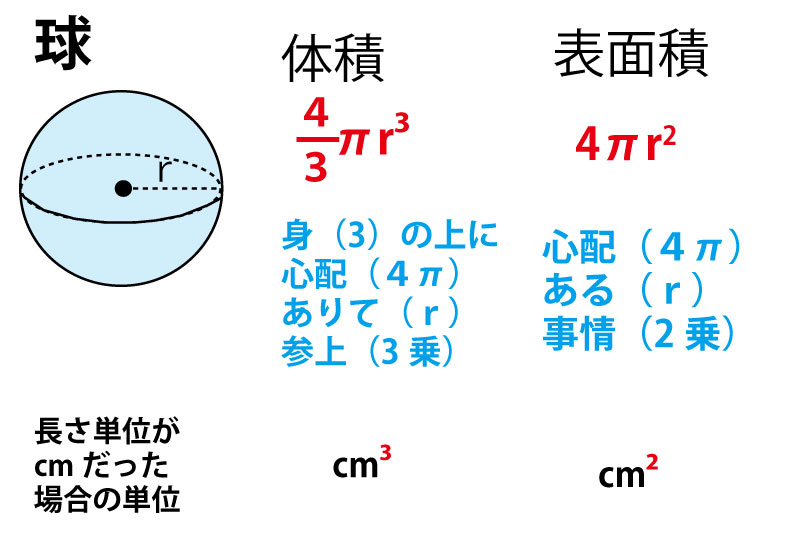
球体 体積 計算-SΔr = （大きな球の体積）− （小さな球の体積） = 4 3π(r Δr)3 − 4 3πr3 S Δ r = （大きな球の体積） − （小さな球の体積） = 4 3 π ( r Δ r) 3 − 4 3 π r 3 が成立します。 あとは中学生でもできる（できそうな）計算をすることで、球の表面積 4πr 2 を導き出せるのです。 以上が図形における微分の概念です。 なんとなく、分かっていただけたでしょうか？ 詳しくは後日、別記事にて解説する予定球の体積の解説 球の体積は 4/3×円周率×半径×半径×半径=体積 で求めることができます。 円周率をπ、半径をr、体積をVとすると、 V=4/3πr 3 となります。 球の体積を求める公式 体積=4/3×円周率×半径×半径×半径 半径6cmの球の体積は何cm 3 ？ ※円周率を314でおこなう場合 → 4/3×314×6×6×6 → cm 3 ※円周率をπでおこなう場合 → 4/3×π×6×6×6 → 864π 3 → 2πcm 3 単位が違う場合

球の体積と表面積の公式の覚え方 積分での求め方 高校数学の美しい物語

はじめに「形状」を選択して下さい。 計算式 重量(kg) = 体積(mm2) × 比重 × 106 本ツールの計算結果の正確性については細心の注意を払っておりますが、保証するものではありません。 計算結果により、不利益や損害を被った場合においても、当社は一切の責任を負いかねますのでご容赦下さい。 アングル Step1材料を選択又は比重を入力します。 ※は必須入力 球の体積の公式をつかいましょう！ 球の体積の公式は、4πr3 / 3でしたね。 4πr 3 / 3 にr=3を代入します。 4π×3 3 / 3 = 36π・・・（答） となります。 簡単ですよね？ 球の体積の公式は必ず覚えましょう！ 球の表面積に関する問題 下の図のように、半径3の半球があるとき、この球の表面積を求めよ。 解答＆解説 半球（球を2等分したうちの片方）ということに注意しましょう！水槽の体積の計算 例題として、下記の水槽の体積を計算しましょう。 3 ですか。また体積が何リットルか計算してください。 水槽の体積＝30x30x60＝cm 3 水の体積＝30x30x＝cm 3 ですね。上記をリットルに換算しましょう。前述したように、1000cm 3 で1

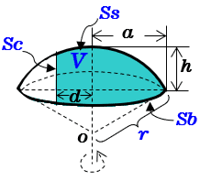
 = 0 とすることで球欠の体積公式： V=\dfrac {1} {6}\pi h (3r^2h^2) V = 61 πh(3r2 h2) が得られます。 球冠，球帯の表面積 高校数学の範囲外ですが，計算は体積より簡単です。 非常に美しい結果です。 球冠，球帯の表面積はその高さに比例する。 注：球帯の高さとは底面と天面の距離です。 球の体積と表面積を積分で証明 の表面積の証明1とほぼ同じことをやるだけです。 証明 もとの b微小面積（体積）を幾何学的に計算して積分する方法 cヤコビ行列を使用する方法 チェックを入れた方法(aとbとcの方法）で計算して、公式と一致しているかどうかを確認しようと思います。 ここでは、「(1b)について説明する」と書けば、「1円の面積」を「b微小面積（体積）を幾 密度、質量、体積の換算の計算問題を解いてみよう それでは、密度、質量、体積の変換に慣れるためにも、計算を行っていきましょう。 まずは、質量と体積から密度を求める問題を解いてみます。 質量と体積から密度を計算する方法 例題1 ある材料の体積cm3であり、その質量

球体 体積 計算のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

球の表面積の公式の求め方	球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	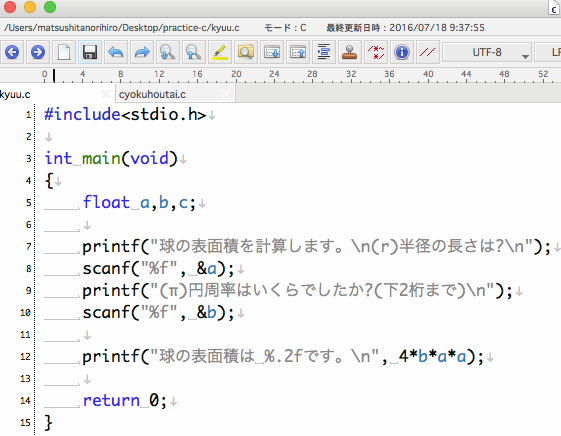球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	球の表面積の公式の求め方	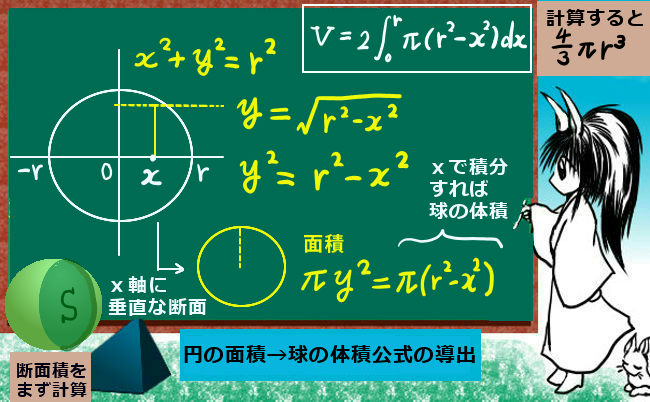球の表面積の公式の求め方
球の表面積の公式の求め方	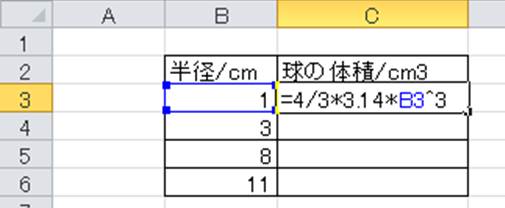球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	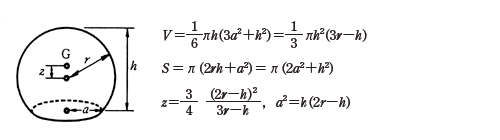球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	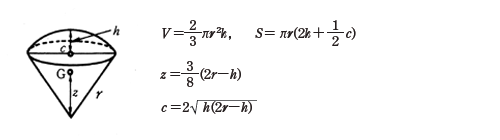球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	球の表面積の公式の求め方	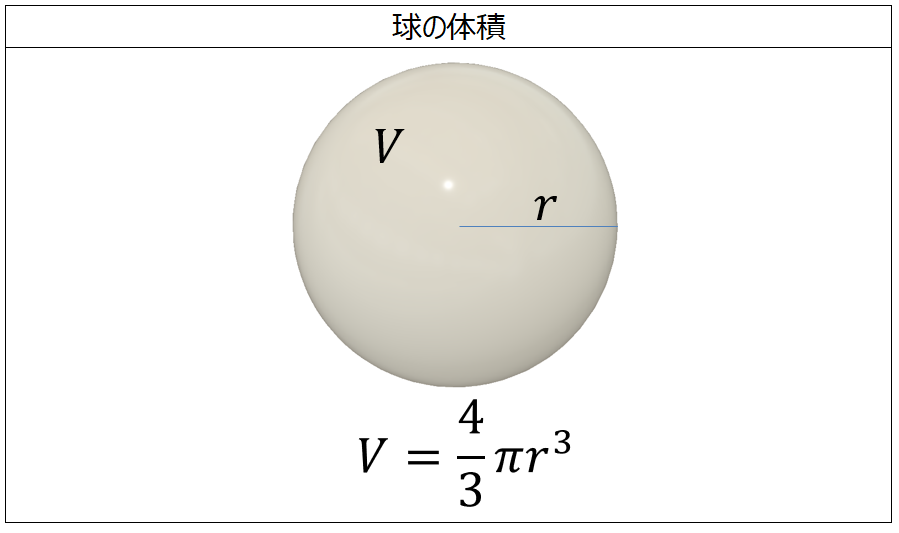球の表面積の公式の求め方
球の表面積の公式の求め方	球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	球の表面積の公式の求め方	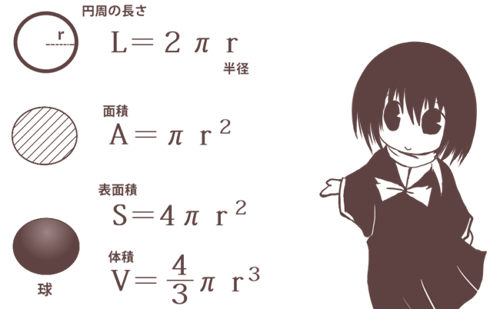球の表面積の公式の求め方
球の表面積の公式の求め方	球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	球の表面積の公式の求め方	球の表面積の公式の求め方
球の表面積の公式の求め方	球の表面積の公式の求め方

実行結果です。 球の半径を入力 r = 10 球の体積 V = 球の表面積 S = ここでは半径「10」の球の体積と表面積を計算してみました。 その他のサンプルプログラムも合わせてご覧ください。 C言語のサンプルプログラム集 C言語の基本構文についV = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S 1 = 角錐底面積 S 2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体

Incoming Term: 球体 体積 計算式, 球体 体積 計算,